❯ Notes On: Statistics Part II (Hypothesis Testing, Chi-Square, ANOVA, Regression)

Category: Science

Series: Notes On

The Notes On series are different from the normal writing here. It's a series about just that: semi-structured notes on a specific topic. Less designed and refined, more exploration and learning.

Statistics is the game of making decisions. If you're interested in making more effective decisions, statistics is for you. This is the second (and last) part in our "Notes On: Statistics" series. Enjoy.

Here are the resources we're using:
Learning Resource: Statology
Practice Dataset: Imported and cleaned Google Sheet (Original from Kaggle here)
Note: For practice, I'll be using Python to analyze the data. If you're following along, analysis can be done in Google Sheets.

Part one can be found here. Topics: Hypothesis Testing, Chi-Square, ANOVA, Regression.
Part two topics: Describing and Visualizing Data, Probability, Study Design, Random Variables, Sampling, Distribution.

HYPOTHESIS TESTING

Hypothesis - assumption about a population parameter
Hypothesis Test - forma statistical test we use to reject (or fail to reject) a hypothesis.

Two types:
(1) Null hypothesis (H0) - hypothesis occurs purely from chance; no effect or difference between old and new method.
(2) Alternative hypothesis (H1 or Ha) - hypothesis is influenced by some non-random cause; there is an effect between the old and new method.

For most statistical tests, we're interested in the p-value.
P-value = strength of evidence in support of a null hypothesis.

P value < significance level, reject the null hypothesis. Opposite, accept the null.
"Since this p-value (0.01) is less than our significance level α = 0.05, we reject the null hypothesis."

Can be calculated by hand, but often calculated by software.

Small effect sizes can produce (impractical) significant p-values when:
(1) Variability in the sample data is very low.
(2) Sample size is very large.

To combat this:
(1) Defining a minimum effect size before conducting a test
(2) Use Confidence Intervals to determine practical significance.

Effect size = quantified difference between the two groups. Goes hand-in-hand with P-Value. Different calculations for effect size include:

(1) Standardized mean difference (Cohen's D is most popular - d of <=0.2 is small, ~0.5 is medium, >=0.8 is large)
(2) Correlation Coefficient (-1 to 1; 0 is no linear correlation - r of ~0.1 is small, ~0.3 is medium, >=0.5 is large)
(3) Odds ratio (further away from 1, higher likelihood of effect)

Benefits of effect sizes over p-values
(1) Gives idea of how large difference / strong association is; p-value only tells us if there is a significant difference / association.
(2) Quantitively compare results of different stories in different settings (p-values cannot do this).
(3) Stronger indicator of practical significance.

Bayes Factor - alternative to p-value; ratio of the likelihood of one particular hypothesis (alternative) versus another (null).
"Bayes factor of 5 means the alt. hypothesis is 5 times as likely as the null hypothesis"

Use thresholds to decide on null hypothesis rejection; thresholds in 2015 defined by Lee and Wagenmaker.

Statistical tests consists of five steps:
(1) State hypothesis (null plus alternative)
(2) Determine a significance level (usually .01, .05, .1).
(3) Find the test statistic and corresponding p-value.
(4) Reject, or fail to reject, the null hypothesis (not up to random chance or not up to random chance) based on p-value.
(5) Interpret the result.

Decision errors with hypothesis testing
(1) Type I Error (False positive): reject the null hypothesis when it actually true. Probability to do so is equal to significance level.
(2) Type II Error (False negative): reject the null hypothesis when it is actually false. Probability is called the Power of the test.

Significance can be statistical or practical
(1) Statistical - indicates effect based on some level of significance (analysis).
(2) Practical - whether or not the effect has practical, real world implications (SME).

Tails in Hypothesis test.
(1) One tailed hypothesis - involves "greater than" or "less than" statement.
(2) Two tailed hypothesis - involved "equal to" or "not equal to" statement.

HYPOTHESIS TEST TYPES

(1) One Sample T-Test - Test whether or not the mean of a population is equal to some value, and if it the difference is statistically significant.

Null hypothesis: always two tailed (equal to)
Alternative hypothesis: can be two-tailed or one tailed (left tailed as less than, right tailed as greater than)

Assumptions:
(A) Variable studied should be either an interval or ratio.
(B) Observations in sample should be independent
(C) Variable studied should be approx. normally distributed
(D) Variable studied should have no outliers.
(2) Two Sample T-Test - Test whether or not two population means are equal, and if it the difference is statistically significant.

Null hypothesis: always two tailed (equal to)
Alternative hypothesis: can be two-tailed or one tailed (left tailed as less than, right tailed as greater than).

Assumptions:
(A) Observations between two samples should be independent of each other.
(B) Two variables studied should be approx. normally distributed
(C) Two variables studied should have approx. same variance (if not: use Welch's t-test)
(D) Data in both samples was obtained using a random sampling method.
(3) Welch's T-Test - Used in place of Two Sample T-Test when variances are not assumed to be the same. Normally, default to this test over Student's T-Test.
(4) Mann-Whitney U Test - Test differences between two independent samples with not-normal distribution and small size (n < 30).

Assumptions:
(A) Variables studied should be either ordinal or continuous
(B) Observations between two samples should be independent of each other.
(C) Distribution between two samples should be roughly the same.
(5) Paired Samples T-Test - Test to compare the means of two samples when each observation in one sample can be paired with the other sample's observations.
Typical use cases:
(A) Measurement taken on a subject before and after treatment (eg. Max vertical jump after training)
(B) Measurement taken under two different conditions (eg. Patient response time measured on two different drugs).

Null hypothesis: always two tailed (equal to)
Alternative hypothesis: can be two-tailed or one tailed (left tailed as less than, right tailed as greater than).

Assumptions:
(A) Participants are randomly selected.
(B) Differences between the pairs should be approx. normally distributed.
(C) Variables studied should have no outliers.
(6) Wilcoxon Signed Rank - Same as Paired Samples T-Test, but with a non-normal distribution.

Assumptions:
(A) Participants are randomly selected.
(B) Variables studied should have no outliers.
(7) One Sample Z-test - Test whether the mean of a population is less than, greater than, or equal to a specific value.

Null hypothesis: always two tailed (equal to, not equal to)
Alternative hypothesis: can be one tailed (left tailed as less than or greater than equal , right tailed as less than equal or greater than).

Assumptions:
(A) Population standard deviation is known.
(B) Variables studied should be continuous (not discrete).
(C) Variables studied should be a simple random sample.
(D) Variables studied should be approx. normally distributed.
(8) Two Sample Z-Test - Test whether two population means are equal.

Null hypothesis: two population means are equal.
Alternative hypothesis: two population means are not equal.

Assumptions:
(A) Population standard deviation is known.
(B) Variables studied should be continuous (not discrete).
(C) Variables studied should be a simple random sample.
(D) Variables studied should be approx. normally distributed.
(9) One Proportion Z-Test - Compares observed proportion to a theoretical one, and if the difference is statistically significant.

Null hypothesis: two tailed (proportion equal to hypothetical proportion)
Alternative hypothesis: two-tailed or one tailed (not equal, less than, greater than)
(10) Two Proportion Z-Test - Test for a difference between two population proportions, and if the difference is statistically significant.

Null hypothesis: two tailed (equal to)
Alternative hypothesis: two-tailed or one tailed (not equal, less than, greater than)

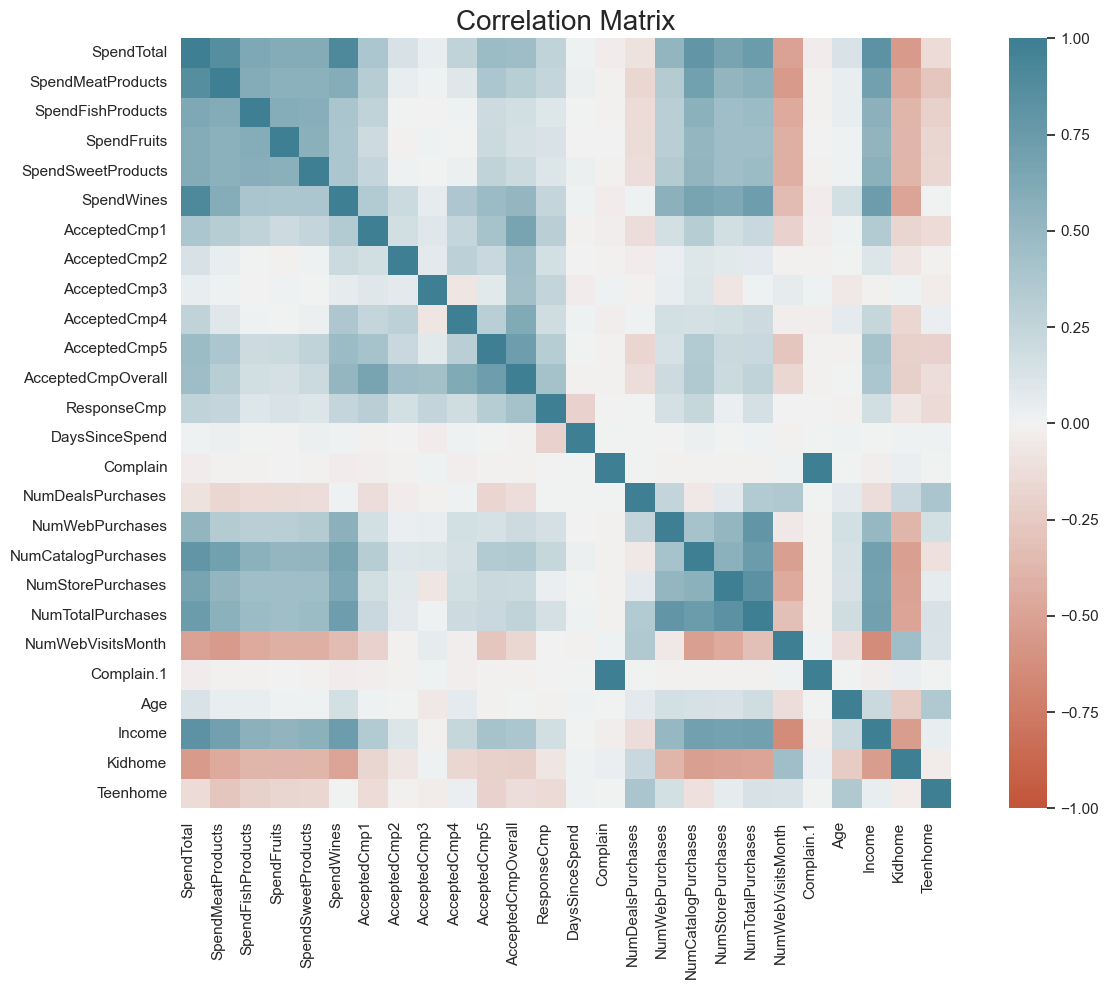
CHI-SQUARE

(1) Chi Square Goodness to Fit - used to determine if a categorical variable follows a hypothesized distribution.
Examples: Distribution of dice rolls, distribution of shoppers in a store by day, percentage of M&Ms by color in a bag.

Null - follows hypothesized distribution
Alternative - does not follow a hypothesized distribution
(2) Chi-Square Test of Independence - determines if two categorical variables have a significant association.
Examples: Gender and political party affiliation, link between favorite color and favorite sport, link between education level and marital status.

Null - two variables are independent
Alt - two variables are not independent (associated)

Effect size with Chi-Square can be measured in three ways:

(1) Phi - used when working with a 2x2 table; interpreted by value of phi.
(2) Cramer's V (V) - used when working with a table larger than 2x2; interpret based on degrees of freedom.
(3) Odds Ratio (OR) - used when working with a 2x2 table; interpreted by distance the odds ratio is from one.

ANOVA / ANALYSIS OF VARIANCE

(1) One-way ANOVA - compares means of three or more independent groups to determine statistically significant difference (or not) between corresponding population means.
Example: Did three different exam prep programs lead to different mean scores on a college entrance example?

Null hypothesis = all population means are equal.
Alt hypothesis = at least one population mean is different than the rest.

Outputs:
(A) Regression sum of squares (SSR)
(B) Error sum of squares (SSE)
(C) Total sum of squares (SST)
(D) Regression degrees of freedom (df(r))
(E) Error degrees of freedom (df(e))
(F) Total degrees of freedom (df(t))
(G) Regression mean square (MSR)
(H) Error mean square (MSE)
(I) F (F)
(J) P-value (P)

Assumptions:
(A) Normality (if not normal, look at Kruskal Wallis test)
(B) Equal Variances
(C) Independence: observations in each group are independent of each other
(2) Two-way ANOVA - compares means of three or more independent groups to determine statistically significant difference (or not) that have been split on two variables (or factor).

Example: Botanist wants to know how sunlight exposure and watering frequency affect plant growth. (Response variable = plant growth, factors = sunlight exposure, watering frequency).

Outputs:
Similar to One-way ANOVA

Assumptions:
(A) Normality
(B) Equal Variances
(C) Independence: observations in each group are independent of each other
(3) Three-way ANOVA - compares means of three or more independent groups to determine statistically significant difference (or not) that have been split on three variables (or factors).

Example: Same as two-way ANOVA, but add fertilizer type.
(4) Repeated Measure ANOVA - compares means of three or more non-independent groups to determine statistically significant differences (or not), in which the same subjects show up in each group.

Typically, two use cases:
(A) Experiments with three or more time periods (eg. Affect training program before, during, and after the program)
(B) Experiments with three or more conditions (eg. Watch three different movies, rate each one).

For all of these tests:
Post hoc test (multiple comparison test) - if the p-value is statistically significant, run post hoc test to determine which groups are different from each other; controls for family-wise error (leads to lower statistical power).

(5) ANCOVA - compares means of three or more independent groups after accounting for one or more covariates (continuous variable that "co-varies" with the response variable).

Assumptions:
(A) Covariate(s) and factor variable(s) are independent
(B) Covariate(s) are continuous data
(C) Homogeneity of variances
(D) Independence: observations in each group are independent of each other
(E) Normality
(F) No extreme outliers

REGRESSION

(1) Simple Linear Regression - understand the relationship between two variables (x and y). To run, follow steps in "Statistical tests consists of five steps".

X = predictor, independent, explanatory.
Y = Response, dependent, outcome.

Assumptions:
(A) Linear Relationship: linear relationship between X and Y.
(B) Independent: residuals are independent.
Residuals are the differences between the data points and the line of best fit (existing or predicted?). Meaning, the value of one residual does not depend on the value of another residual. It's a check for errors; error for predicting one data point could mean errors for others, reducing accuracy.
(C) Homoscedasticity: Residuals have constant variance at specific levels of X.
(D) Normality: Residuals are normally distributed.

Plot X vs Y to visualize relationship; (linear) regression comes in to quantify the relationship (ie. for an increase in X, we expect to see a # change in Y.)

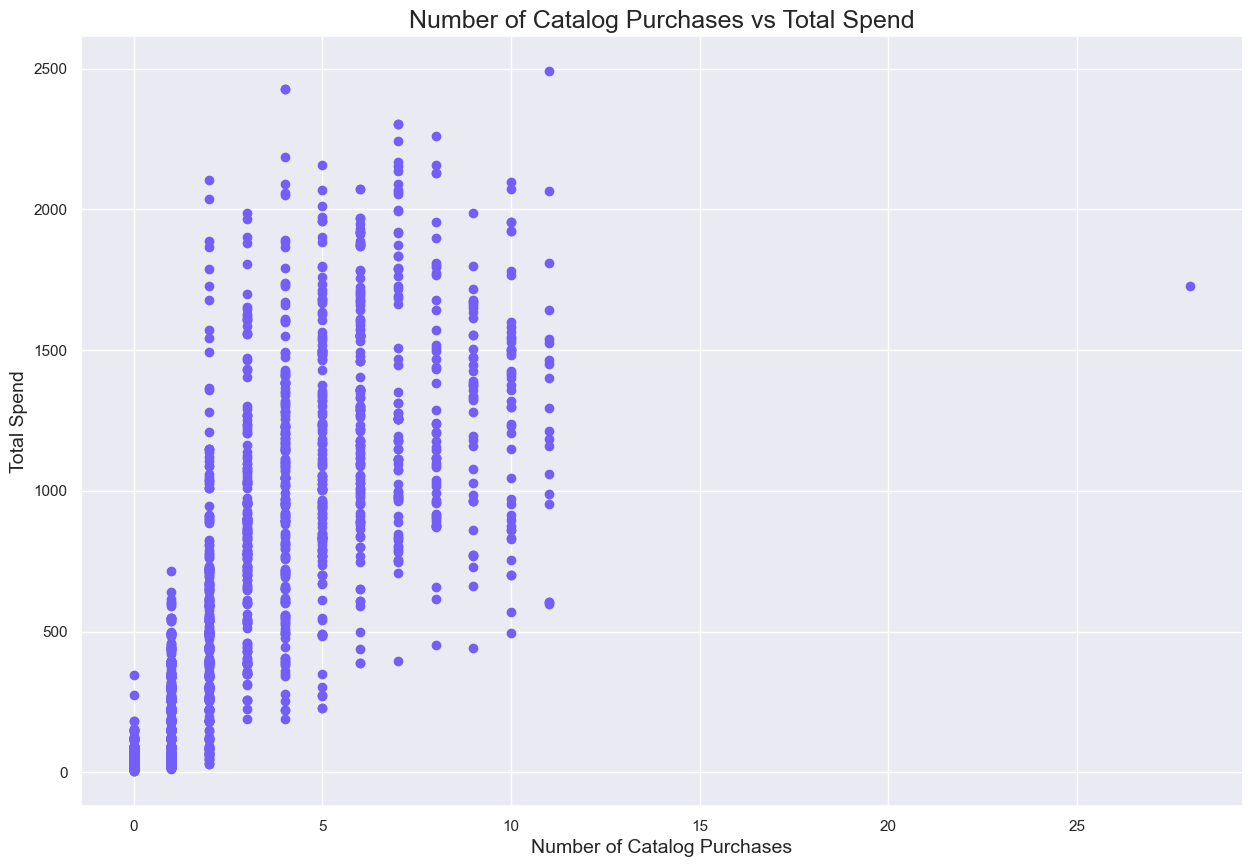
Least Squares Regression Line - best fit to our data, helps us better quantify and understand the relationship between X and Y (slope of a line formula?)

Formula: y = a + bx
Example: y = 32.7 + 0.2x; "a" = when the predictor variable is zero, the starting value of "a" is 32.7. "b" = with an increase of one unit of X, there is a 0.2 unit increase in the response variable.

Starts getting predictive (eg. for a person who weights 150 pounds, how tall would we expect them to be?)
Coefficient of Determination (R^2) - how well does the Least Squares Line Fit the data?Another way to say: how well is the variance in the response variable explained by the predictor variable?

0 = response variable cannot be explained at all by predictor.
1 = response variable perfectly explained, without error, by predictor. (eg. 0.2 = 20% of response variable variance explained by predictor).
(2) Multiple Linear Regression - extremely similar to Simple Linear regression; input multiple predictor variables to understand a response variable. To run, follow steps in "Statistical tests consists of five steps"

Typical Outputs:
(A) Coefficients: interpretation for MLR; uses formula above.
(B) Coefficient of Determination (R^2): see above Simple Linear Regression Model for explanation.
(C) Standard Error (S): Average distance observed values fall from regression line. Used to assess fit. Smaller standard error, the better a model is able to fit the data. (Careful of overfitting).
(D) F: How well does the overall regression model fit the data? Basically, are all of the predictor variables jointly significant or not? (Large = fits, small = doesn't fit)
(E) Significance F: Is the overall model significant?
(F) Coefficient P-values: Is each predictor variable statistically significant?

Assumptions:
(A) Linear Relationship: linear relationship between X and Y.
(B) Independent: residuals are independent. (See above Simple Linear Regression Model for explanation)
(C) Homoscedasticity: Residuals have constant variance at specific levels of X.
(D) Normality: Residuals are normally distributed.

Watch out: Multicollinearity - >=2 predictor variables are highly correlated, causing problems with fit and interpretation, as those variables tend to change in unison. The coefficient estimates can fluctuate and have reduced precision (unreliable p-values -> determining statistical significance).

Detect with Variance Inflation Factor (VIF) (Always run?).

Resolving problems:
(A) Remove one or more of the highly correlated variables.
(B) Linearly combine the predictor variables in some way.
(C) Perform analysis designed to account for highly correlated variables (eg. Principal component analysis or partial least squares regression).

Watch out: Heteroscedasticity - residuals do not have constant variance; run Breusch-Pagan test to determine if Heteroscedasticity is present.

Snapshot:

Screen-time at the Pichichero household is limited. Only in the evenings, before bed, and sixteen minutes (two episodes of Bluey).
Tonight, the end credits rolled.
"Bedtime," we declared.
"Play more. For two minutes," was your instant response.
You have no idea what two minutes means… but we let you have it anyway.

Striving for better,

Justin Pichichero