❯ Notes On: Statistics (EDA, Probability, Study Design, Sampling, and Distribution)

The Notes On series are different from the normal writing here. It's a series about just that: semi-structured notes on a specific topic. Less designed and refined, more exploration and learning.

Before we begin, why Statistics? If you're in the game of making decisions, Statistics is for you. I've found knowing the basic language and use cases of functional knowledge (like statistics or engineering) has enabled me to be a more effective leader—whether that's been direct team leadership or as an adjacent partner.

Without further ado.

Here are the resources we're using:
Learning Resource: Statology
Practice Dataset: Imported and cleaned Google Sheet (Original from Kaggle here)
Note: For practice, I'll be using Python to analyze the data. If you're following along, analysis can be done in Google Sheets.

Part one contains: Describing and Visualizing Data, Probability, Study Design, Random Variables, Sampling, Distribution.

Foundation

Statistics: collection, analysis, interpretation, and presenting data (quantitative or qualitative). Important to:
(1) Understand the world.
(2) Catch misleading charts and data.
(3) Anticipate confounding variables.
(4) Make better decisions (and predictions) with probability.
(5) Understand p-values and correlation.
(6) Notice bias and assumptions.
(7) Avoid overgeneralization or non-representation.

Two branches of statistics:
(1) Descriptive Statistics: describes existing data; concerned with what happened in the past.

• Three common forms of descriptive statistics:
  (A) Summary: summarize data with single numbers.
  Usually, measure of central tendency (finding the center of a dataset; ie. mean, median, mode) and dispersion (spread of values in a dataset; ie. range, standard deviation, variance).
  (B) Graphs: visualize data.
  (C) Tables: distribution of data (ie. Frequency table).

(2) Inferential Statistics: make inferences about a large population based on small sample of data. Testing hypotheses and making predictions lives here.

• Statistic = number that describes a sample's characteristic.
  Parameter = number that describes a population's characteristic.
  The closer our statistic can get to the parameter, the better.
  Population = every possible individual (or element) that we are interested in measuring.
  Sample = a subset or portion of the population.
  
  Population parameters we're most commonly interested in:
  (1) Population mean: mean value of X variable in a population.
  (2) Population proportion: proportion (%) of some variable in a population.

Confidence interval - captures uncertainty (mean, difference between means, etc.); range of estimate that likely contains the value with a certain level of confidence.

Larger sample = narrower confidence interval.
Higher confidence level = wider confidence interval.
"There is a (Z value -> % chance) that the confidence interval of (high bound, low bound) contains the true population mean of (variable)."

• Most common confidence intervals (CI):
  (1) Mean CI: contains population mean.
  (2) Difference between Means CI: contains true difference between two population means.
  (3) Proportion CI: contains population proportion.
  (4) Difference between proportions CI: contains true difference between two population proportions.
  (5) Standard deviation CI: contains population standard deviation.

Central limit theorem - sampling distribution of mean is approximately normal if the sample size is large enough, even if the population distribution is not normal (woah).

Normality - sampling distribution of mean is normal in most cases with a sample size of 30 or greater. For sampling distribution of proportion, normal if success and failure are both at least 10.

Other common properties:
(1) mean of the sampling distribution will be equal to the mean of the population distribution.
(2) Variance of sampling distribution will be equal to the variance of the population distribution divided by the sample size.

Sampling

Sample = a subset or portion of the population. Used for time, data, and feasibility in data collection.
Sampling distribution of mean = mean of sample will be close, but have some variance compared to the population.
There is an equivalent for the proportion (percentage).
Sample frame = list or source from which you will select your sample participants. Needs unique identifier and contact method.

• Sampling frame error - drift from target population and sample from the sample frame (sample will not be perfectly representative).
  Usually, there is some drift from target population and sample from the sample frame (ie. Someone moved, but frame hasn't been updated to reflect the change).

Representative sample = mirrors intended population as closely as possible. Representation is good to generalize findings with confidence.
Size of sample important for representation. To determine needed size, look at: overall population size, confidence level, acceptable margin of error.

Non-representative sample = cannot generalize findings; conclusions and predictive ability isn't valid.

Common sampling methods for representative samples:

• (1) Simple Random - randomly selection of individuals.
  (2) Systematic random - put every individual of a population in order of some characteristic, choose a random starting point, then select every nth member be in the sample.
  (3) Cluster random - divide groups into their natural clusters, then random sample each cluster and include all members of the selected clusters in the samples.
  (4) Stratified random - split a population into groups. Randomly select some members from each group to be in the sample.

Advanced sampling methods

• (A) Latin Hypercube - divide cumulative density function into X equal partitions, then choosing a random data point in each partition.
  Generates controlled random samples; applied to Monte Carlo analysis.
  Main advantage - samples reflect underlying distribution (especially with high dimensions), requires much smaller sample sizes that simple random sampling.

Not-great sampling methods (high potential for non-representative sample):

• (1) Convenience sample - choose readily available subjects
  (2) Voluntary response sample - subjects voluntarily decide to be included in the sample or not.
  (3) Snowball sample - ask initial subjects to recruit additional subjects.
  (4) Purposive sample - researchers recruit specific, likely biased subjects.

Three common forms of inferential statistics:

• (1) Hypothesis test: draw conclusions to questions about a population.
  (2) Confidence interval: a range of values that we're confident the true population's characteristic falls within.
  (3) Regression: understand the relationship between two (or more) variables.
  

Variables and Measurement Scales

(1) Quantitative variables = Numerical, measurable (ie. person's height or age). Summarized with measures of central tendency and dispersion.
(2) Qualitative variables = categorical, names or labels (ie. person's eye color or name). Summarized with relative frequency table.

Measurement Scale

Examples
Nominal = eye color, blood type
Ordinal = satisfaction, degree of pain
Interval = temperature, credit or SAT score
Ratio = height, weight, length

Describing and Visualizing Data

Describing Data

• (1) Measure of Central Tendency - single value representing a dataset's central point; purpose is quicker comprehension.
  (2) Mean - the average value (sum of all values / total # of values). Used when data is symmetrical and there are no outliers.
  (3) Median - middle value in sorted dataset. Used when data is skewed or outliers are present.
  (4) Mode - value that occurs most often in a dataset (no, one, or multiple allowed). Used with categorical data.
  (5) Measure of Dispersion - measures the spread of values in the dataset.
  (6) Range - difference between the largest and smallest value in a data set.
  (7) Interquartile range - difference between the first and third quartile in a dataset. More resistant to outliers versus range.
  (8) Variance - how far is each number from the mean and from every other number in the data set.
  (9) Standard deviation - average amount of variability in your dataset; how far does each data point lies from the mean.

Describing data distributions with SOCS
Shape - normal or skewed distribution and unimodal or bimodal peaks?
Outliers - any outliers present?
Center - mean, median, mode?
Spread - range, interquartile range, standard deviation, and variance.

Data Visualizations

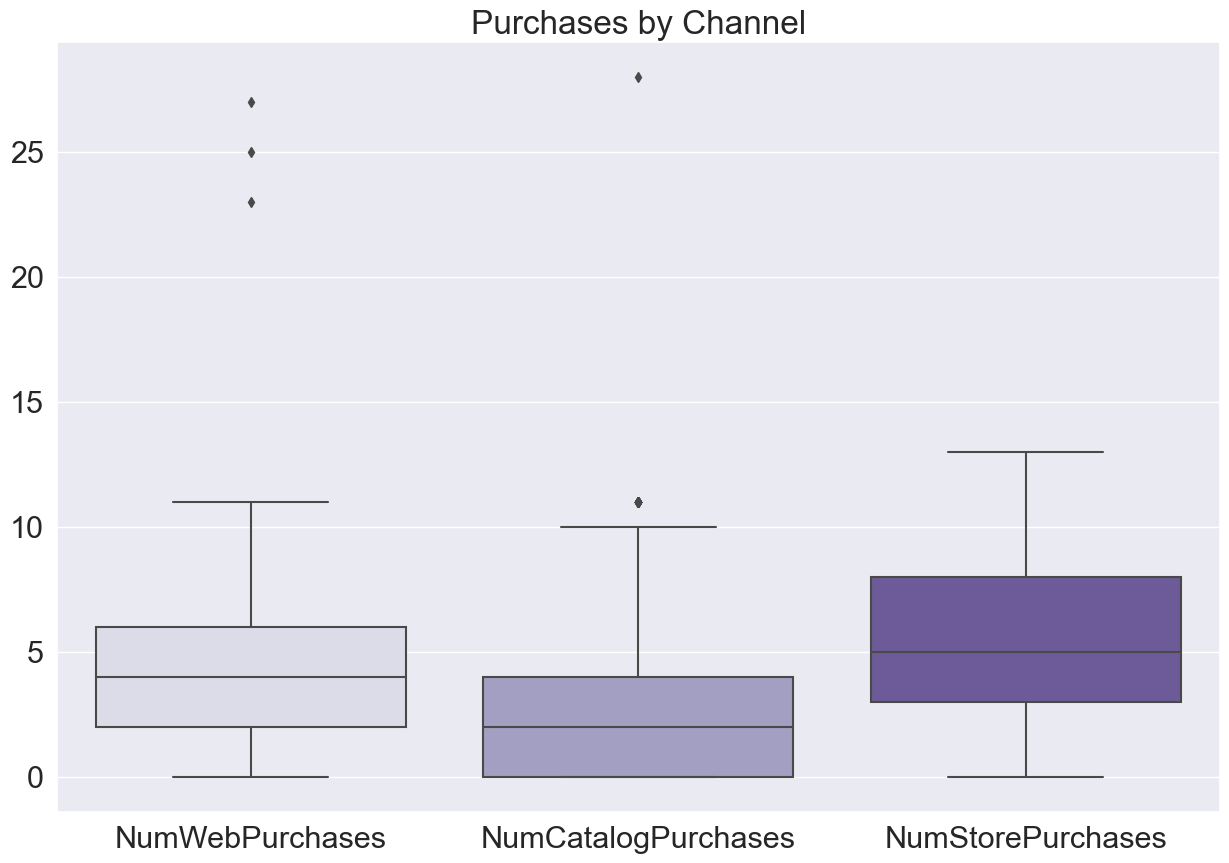
• (1) Boxplot - useful to show five descriptive stats (minimum, lower quartile, median, upper quartile, maximum).
  (2) Stem and leaf - I will never use this.
  (3) Scatterplots - useful to show relationship (positive or negative association by direction) and strength between two variables (the correlation).
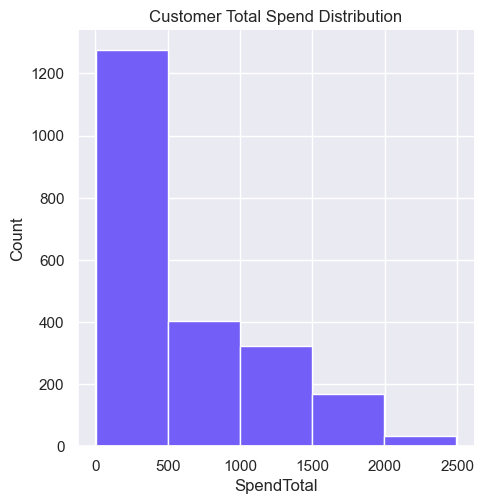
  (4) Relative Frequency Histogram - useful to show often a certain event occurred in the data set; relative uses percentage of each event relative to the whole.
  (5) Density Curves - useful to show distribution of values in a dataset (ie. famous bell-shaped curve).

Other helpful characteristics of Density Curves:
(1) Shows shape of distribution (peaks, skewed).
(2) Shows mean and median.
(3) Percentage of observations that fall between certain values.

Interpreting Data Visualizations:

• (1) Skew - left or negative skew has a tail to the left (peak to the right); right or positive skew has a tail to the right (peak to the left); no skew has a peak in the middle.
  (2) Mean and median - left skewed curves, the mean is less than the median; right skewed curves, the mean is greater than the median; no skew, mean and median are equal.
  (3) Peaks - single peak is unimodal; two peaks is bimodal; two or more is called multimodal distribution.

Probability

Probability - the likelihood of certain events happening. Two of the most common areas:
(1) Theoretical Probability - likelihood of event to occur based on pure math.

• P(A) = (number of desired outcomes) / (total number of possible outcomes)
  Usually faster to calculate than experimental probability.

(2) Experimental Probability - actual probability of an event occurring that you directly observe in an experiment.

• P(A) = (number of times event occurs) / (total number of trials)
  Usually easier to calculate than theoretical probability.

Others probability includes:

• (1) Prior probability - probability of an event with all known, established information. (Bayesian statistical inference?)
  (2) Posterior probability - updated probability of an event after accounting for new information.
  P(A|B) = (P(A) * P(B|A)) / P(B)
  (3) Odds ratio - the ratio of two odds; Useful to understand potential outcomes (ie. new treatment vs old; marketing campaign vs no campaign).
  Ratio = (Odds of Event A) / (Odds of Event B)
  (4) Law of large numbers - larger sample size = sample mean gets closer to the expected value (ie. outcome of coin flips after 5 tries versus 200 tries. Other examples include casinos, insurance, and renewable energy).
  (5) Set operations - set is a collection of items (ie. A = {1, 2, 3} - array?).
  (6) General Multiplication Rule - calculates the probability of any two events occurring. "the probability that B occurs, given that A has occurred"; can imagine this is helpful for lottery / powerball.
  P(A and B) = P(A) * P(B|A)
  

Types of Set Operations
(What SQL is based on?)

• (1) Union - Set of items in either A or B (notation: A u B)
  {1, 2 , 3} u {4, 5, 6} = {1, 2, 3, 4, 5, 6}
  
  (2) Intersection - Set of items in both A and B (notation: A n B)
  {1, 2, 3} n {3, 4} = {3}
  
  (3) Complement - Of Set A, in the set of items that are in thee universal set U but not in A. (notation: A' or A^c)
  If U = {1, 2, 3} and A = {1, 2}, then A' = {3}
  
  (4) Difference - Set of items in A but not B (notation: A - B)
  {1, 2, 3} - {2, 3, 4} = {1}
  
  (5) Symmetric Difference = Set of items in either A or B, but not both (notation: A delta B)
  {1, 2, 3} delta {2, 3, 4} = {1, 4}
  
  (6) Cartesian Product = Set of ordered pairs from A and B (notation: A x B)
  If A = {H, T} and B = {1,2, 3}, then = {H(H, 1), (H, 2), (H, 3), (T, 1), (T, 2), (T, 3)}
  

Study Design

Context
First, knowing variable types are important.

• (1) Explanatory variable - independent or predictor variable; explains the variation in the response.
  (2) Response variable - dependent or outcome variable; responds to changes from explanatory variable.
  (3) Lurking variable - variable not account for in an experiment that could potentially affect the outcome.

Values of explanatory variable are changed to observe effects on response variable.

Design Types
(1) Matched Pairs - used when an experiment only has two treatment conditions. Randomly match pairs based on a common variable (ie. Gender or age / age range), then subjects are randomly assigned to different treatments.

• Advantages
  (A) Controls for lurking variable.
  (B) Eliminates order effect (order effect is differences in outcome due to order in which experimental materials are presented) because each subject only receives one treatment.
  
  Disadvantages
  (A) Losing two subjects if one drops out.
  (B) Time-consuming to find matches.
  (C) Impossible to perfectly match subjects .

(2) Pre-test & Post test - measurements taken on individuals both before and after they are involved in some treatment.

• Often, process is pre-test -> treatment -> post-test -> analyze differences (ie. School testing).
  Quasi-experiment, the process can be done by itself. In a true experiment, it will be done in addition to the standard treatment.
  
  Issues with internal validity - reliability of cause-and-effect relationship of treatment and outcome. Factors affecting it: History, maturity, attrition, regression to the mean, selection bias.
  
  Random selection and random assignment can combat internal validity.

(3) Split-plot - two factor that have differing complexity (one factor is hard to change, the other is easy). Usually in manufacturing or agriculture (high capital sectors).

• Advantages
  (A) Cost - one factor doesn't have to be changed in each split-plot.
  (B) Efficiency - more efficient to run, with increased precision.
  
  Disadvantages
  (A) Complex - upfront complexity to set up the experiment.

(4) Permuted Block Randomization - technique to randomly assign individuals to certain treatments within a block (ie. Split-plot above).

(5) Binomial experiments - think coinflip; has the following properties:

• Experiment consists of X repeated trials.
  Each trial only has two possible outcomes.
  Probability of success is the same for each trial.
  Each trial is independent from the others.

(6) Poisson experiments - think births/hour at a given hospital; has the following properties:

• Number of successes in the experiment can be counted.
  Mean number of successes during a specific interval of time is known.
  Each outcome is independent.
  Success probability is proportional to the size of the interval.

Random Variables

Random variable (denoted: X) - variable whose possible values are outcomes of a random process.

Two Types of Density Functions
(1) Probability density function (PDF) - probability that a random variable takes on a certain value. Cannot use directly with continuous random (because X takes on any exact value is zero)

(2) Cumulative density function (CDF) - probability that a random variables takes on a value less than or equal to X. Can be used directly with continuous random.

Two types of Random Variables.

(1) Discrete Random - Variable that can take on a finite number of possible values (ie. Number of defective widgets in a box of 50 widgets).

• Probability distribution for Discrete - probability that the random variable takes on certain values (ie. 6-sided dice rolling landing on 2 would be 1/6).
  Cumulative Probability distribution for Discrete - probability that the random variables take on a value equal to or less than another value. (ie. 6 sided dice rolling landing on 2 would be 2/6).

(2) Continuous Random - Variable that can take on an infinite number of possible values (ie. Weight of an animal, height of a personal, marathon time).

• Probability distribution for Continuous - only tells us the range the values can take.

Rule of thumb: count the number of outcomes? Discrete. Measure the outcome? Continuous.

Types of distributions

Note: Formula definitions primarily from Statology, edited out formulas for friendly web viewing. Helpful to refer to skew above.

(1) Normal distribution - bell shaped, symmetrical, mean / median are equal and located at the center.

• Empirical Rule (68-95-99.7) - distribution of data.
  68% of data falls within one standard deviation of mean.
  95% of data falls within two standard deviations of mean.
  99.7% of data falls within three standard deviations of the mean.

(2) Binomial distribution - number of successes in a fixed number of independent trials with two possible outcome (success / failure; Bernoulli trial).

(3) Poisson distribution - number of successes during a given time interval.

(4) Geometric distribution - likelihood to experience a number of failures before experiencing the first success in Bernoulli trials

(5) Uniform distribution - every value between an interval (a to b) is equally likely to occur.

(6) Exponential distribution - models the time we must wait until a certain event occurs. Memoryless property.

(7) Hypergeometric distribution - probability to choose objects with a certain feature in fixed number of draws (no replacements) from a finite sized population that contains X objects with aforementioned feature.

(8) Negative Binomial distribution - probability to experience X number of failures before experiencing Y number of successes with two possible outcome (success / failure; Bernoulli trial).

(9) Multinomial distribution - obtain a specific number of counts for X different outcomes, where each outcome has a fixed probability of occurring.

Snapshot:

One day, you won't need dad to pack your lunch and Little Blue Truck won't be cool anymore. Until then, I'll enjoy every moment. Happy birthday, son.

Striving for better,

Justin Pichichero